TTC Video – Understanding Multi-Variable Calculus

Understanding Multivariable CalculusAward: Problems, Solutions, & Tips-Professor Bruce H. Edwards, University of Florida, was awarded the Nobel Prize in Calculus. He brings together the basic concepts of calculus in a deeper and more powerful manner.
File size: 13.03GB

TTC Video – Understanding Multi-Variable Calculus

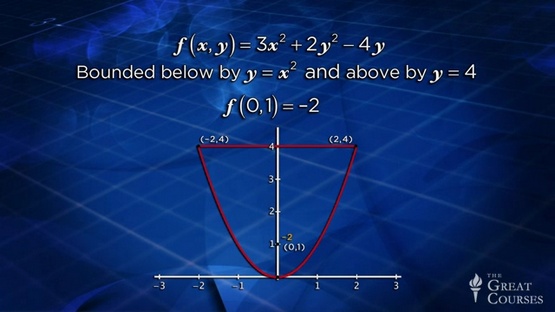
Calculating the volume of odd is possible-Calculus in three dimensions is essential for many things, including predicting the outcome in statistical trials or weather forecasts. Once you grasp the basics of multivariable calculation, you will see how these concepts can be used to create new laws, new fields in physics, and new approaches.-impossible problems.

 We can use multivariable calculus to calculate the ge

• Optimization tools that can take into consideration as many variables as necessary;
• These vector fields give us a glimpse into the workings fluids, from hydraulic pistons to ocean currents or the weather.
• New coordinate systems are available that allow us to solve integrals with Cartesian coordinates.
• Mathematical definitions of surfaces and planes in space are the basis of many fields of mathematics, including topology and differential geometry.

 Understanding Multivariable CalculusAward-winning teachers will teach you how to solve problems and give you tips.-Professor Bruce H. Edwards of University of Florida was the winner. This course brings the basic concepts of calculus together in an even deeper and more powerful way. This course is the next step in the learning process for professionals and students who want to increase their knowledge for work and study in many quantitative areas.-Open intellectual exercise for teachers, retired professionals, or anyone else who wants an understanding of the incredible applications of 3-D calculus.

 This course is for anyone who is familiar with basic calculus. Understanding Multivariable Calculus This is a summary of what follows, but doesn’t essentially require knowledge. Calculus II. II. Calculus II that carry over, like vector calculus are briefly reintroduced here, with a new emphasis placed on three dimensions.

 The 36 comprehensive lectures will focus on the development and generalization of fundamental tools of integration/differentiation to functions of more then one variable. Under the expert guidance of Professor Edwards, you’ll embark on an exhilarating journey through the concepts of multivariable calculus, enlivened with real-Beautiful animated graphics and world examples that take calculus out the textbook and into our three-dimensional world help us to get it right.-Dimensional world.

 A New Approach to Old Problems

 How can you integrate over a particular region? xy plane that can’t be defined by just one standard y = f(x). function? Multivariable calculus has many hidden surprises. It contains the answers to many of these questions. In Understanding Multivariable CalculusProfessor Edwards uses powerful new tools in every lecture. This allows him to solve difficult problems in a few steps and turn complex integrals into simple. It also gives exact answers where calculators cannot.

 These tools will make it possible to:

• Use double or triple integrals to integrate volumes and surfaces directly;
• Use vectors to define parametric equations that are easily differentiable for a function;
• To evaluate double- and triple integrals that are not easy to solve in standard Cartesian coordinates, you can use spherical, cylindrical, or polar coordinates.

 Professor Edwards guides you through these new techniques with clarity and enthusiasm that makes even the most difficult material accessible and enjoyable. With animated graphics featuring state-This is-The-art software that brings you three-This course will bring 3D surfaces and volumes to life. The accompanying illustrated workbook will also help you to understand the full potential of this most important mathematical achievement of humankind.

 About Your Professor

 Dr. Bruce H. Edwards, Professor of Mathematics at University of Florida. Dartmouth College is where he earned his Ph.D. He has received numerous Teacher of Year awards and awards for his contributions to mathematics education in Florida.